Гармонические колебания являются одним из основных типов движения в физике и инженерии. Они характеризуются постоянной амплитудой и постоянной частотой, которая остается неизменной со временем. Основные уравнения гармонических колебаний силы тока и напряжения описывают зависимости этих физических величин от времени.
Уравнение гармонических колебаний силы тока представляет собой синусоидальную функцию вида I = I₀ * sin(ωt + φ), где I₀ - максимальное значение тока, ω - угловая частота, t - время, φ - начальная фаза. Это уравнение позволяет определить значение силы тока в любой момент времени и представляет собой стандартную форму записи для описания электрических колебаний в цепях переменного тока.
Уравнение гармонических колебаний напряжения имеет аналогичный вид V = V₀ * sin(ωt + φ), где V₀ - максимальное значение напряжения. Это уравнение позволяет определить значение напряжения в цепи переменного тока в любой момент времени и является основой для расчетов в электротехнике и электронике.
Гармонические колебания силы тока и напряжения широко применяются в различных областях науки и техники. Они используются в синтезе звука, генерации и передаче электроэнергии, в радиотехнике, связи и других областях, где требуется передача сигналов и энергии с помощью переменного тока и напряжения. Понимание уравнений гармонических колебаний силы тока и напряжения является ключевым для разработки и анализа электрических цепей, проектирования электронных устройств и систем.
Основы уравнений гармонических колебаний

Гармонические колебания являются одним из основных понятий в физике и науке об электричестве. Они возникают в результате действия некоторой силы, которая возвращает систему к равновесному положению после ее отклонения.
Уравнения гармонических колебаний описывают зависимость движения от времени. Они имеют вид:
x = A * sin(ωt + φ)
где:
- x - отклонение от равновесного положения;
- A - амплитуда колебаний (максимальное отклонение);
- ω - угловая частота (в радианах в секунду);
- t - время (в секундах);
- φ - начальная фаза (начальная позиция).
Уравнения гармонических колебаний применяются во многих областях физики и техники. Они позволяют описать колебательные процессы, такие как механические колебания, электромагнитные колебания в электрических цепях и другие.
Важно отметить, что гармонические колебания можно представить как суперпозицию двух гармонических функций, одна из которых сдвинута по фазе на π/2:
x = A * sin(ωt) + B * cos(ωt)
где A и B - амплитуды колебаний.
Уравнения гармонических колебаний являются основой для понимания различных физических явлений и применяются во множестве инженерных и научных задач.
Что такое гармонические колебания?

Гармонические колебания - это тип колебаний, при которых перемещение отклоняющегося от положения равновесия объекта изменяется по синусоидальному закону. Такие колебания характеризуются постоянной амплитудой и постоянной частотой.
Гармонические колебания широко применяются в физике, математике и инженерии. Они играют ключевую роль в описании и анализе различных явлений и систем, таких как механические колебания, электромагнитные волны, электрические цепи и другие.
В гармонических колебаниях основные понятия включают амплитуду, период, частоту и фазу. Амплитуда представляет собой максимальное отклонение от положения равновесия. Период - это время, за которое одно полное колебание происходит от одной крайней точки до следующей. Частота - это количество полных колебаний в единицу времени. Фаза - это положение объекта в отношении точки синусоидального графика.
Гармонические колебания могут быть описаны уравнением гармонического осциллятора, которое связывает силу тока или напряжение с параметрами системы. Это уравнение имеет вид: F = -kx, где F - сила, x - перемещение, k - коэффициент пропорциональности.
Важным примером гармонических колебаний является колебательный контур в электрической цепи. При подключении к контуру источника переменного тока возникают гармонические колебания тока и напряжения. Это явление широко используется в электронике и радиотехнике для передачи и приема сигналов.
В заключение, гармонические колебания представляют собой важный класс колебательных движений, который играет ключевую роль в различных областях науки и техники. Их изучение позволяет понять и описать разнообразные физические явления и является основой для разработки и проектирования различных устройств и систем.
Формула уравнения гармонических колебаний

Уравнение гармонических колебаний описывает движение объекта, совершающего гармонические колебания, такие как колебания маятника или электромагнитного поля.
Формула уравнения гармонических колебаний имеет вид:
x(t) = A*cos(ωt + φ),
где:
- x(t) - расстояние (смещение) объекта от положения равновесия в момент времени t;
- A - амплитуда колебаний, то есть максимальное смещение объекта от положения равновесия;
- ω - угловая частота колебаний, определяющая скорость изменения фазы колебаний. Значение угловой частоты равно 2πf, где f - частота колебаний;
- φ - начальная фаза колебаний, указывающая на положение объекта в момент времени t=0.
Уравнение гармонических колебаний позволяет определить положение объекта в любой момент времени и описывает периодическое поведение системы.
Сила тока и ее связь с гармоническими колебаниями

В физике сила тока представляет собой количественную меру электрического тока, который протекает через проводник. Электрический ток представляет собой движение электрических зарядов через проводник под действием электрической силы.
Гармонические колебания, с другой стороны, являются изменениями величины с течением времени вокруг некоторого равновесного значения. Они имеют определенную амплитуду, период, частоту и фазу.
Сила тока может быть представлена как гармоническое колебание, когда ее значение в течение времени меняется вокруг некоторого равновесного значения. Это означает, что сила тока может быть представлена в виде синусоидальной функции, в которой максимальное значение силы тока соответствует амплитуде колебаний, а период колебаний соответствует периоду текущего электрического сигнала.
Важно отметить, что сила тока может иметь как постоянную, так и переменную величину. В случае постоянной силы тока говорят о постоянном токе, в то время как переменная сила тока описывает переменный ток.
Связь между силой тока и гармоническими колебаниями позволяет анализировать и описывать электрические сигналы и их свойства. Это особенно полезно при изучении электрических цепей и их поведения при воздействии на них различных сигналов и источников питания.
Как работает электрическая цепь?

Электрическая цепь представляет собой замкнутую систему проводников, которая позволяет передавать электрический ток от источника питания к потребителям электроэнергии. В такой цепи электроны, заряженные частицы, двигаются внутри проводников под воздействием разности потенциалов.
Основные компоненты электрической цепи:
- Источник питания: это устройство, которое создает электрическую разность потенциалов и обеспечивает постоянный или переменный ток. Примерами источников питания являются батареи, генераторы и аккумуляторы.
- Проводники: это материалы, которые обладают низким сопротивлением электрическому току. Наиболее распространенным проводником является металл, например, медь.
- Потребители: это устройства или нагрузки, которые используют электрическую энергию для выполнения определенных задач. К ним относятся лампы, моторы, компьютеры и другие электрические устройства.
В электрической цепи ток может быть постоянным или переменным. Постоянный ток (Direct Current, DC) протекает в одном направлении и используется в устройствах, где требуется стабильная энергия, например, в электронных схемах и батарейных устройствах. Переменный ток (Alternating Current, AC) меняет свое направление со временем и используется в электросетях для передачи электроэнергии на большие расстояния.
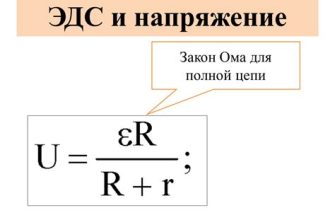
Работа электрической цепи основана на законе Ома, который связывает напряжение, силу тока и сопротивление. Согласно этому закону, сила тока пропорциональна напряжению и обратно пропорциональна сопротивлению. Иными словами, чем больше напряжение или меньше сопротивление, тем больше сила тока будет протекать через цепь.
Чтобы рассчитать силу тока в электрической цепи, необходимо знать напряжение и сопротивление. Формула, описывающая эту зависимость, выглядит следующим образом:
I = U / R
Где I - сила тока в амперах, U - напряжение в вольтах, R - сопротивление в омах.
Таким образом, электрическая цепь является основой для передачи электроэнергии и питания электрических устройств. Современная технология и бытовая электроника невозможны без эффективных и надежных электрических цепей.
Ток как результат гармонических колебаний

В физике существует понятие гармонических колебаний, которые описываются синусоидальными функциями. Такие колебания могут возникать в различных системах, включая электрические цепи.
В электрической цепи, имеющей резистор, индуктивность и емкость, может возникать гармоническое напряжение или ток. Гармоническое напряжение представляет собой переменное напряжение, меняющееся по синусоидальному закону во времени. Аналогично, гармонический ток является переменным током, меняющимся также по синусоидальному закону.
Гармонический ток обычно выражается с помощью комплексных чисел. Он представляет собой комплексное число, состоящее из действительной и мнимой частей. Действительная часть соответствует активной составляющей тока, а мнимая часть – реактивной составляющей.
Активная составляющая гармонического тока выражает мощность, которую потребляет электрическая цепь. Реактивная составляющая отвечает за энергию, хранящуюся и переходящую между элементами цепи.
Гармонические колебания и токи имеют множество применений. Они используются в системах связи для передачи информации с помощью модуляции амплитуды, частоты или фазы гармонического сигнала. Гармонические колебания также используются в музыкальных инструментах для создания различных звуков.
| Область применения | Пример |
|---|---|
| Электротехника | Генерация электрического сигнала |
| Музыка | Создание звуковых волн |
| Связь | Передача информации по проводу или в воздухе |
| Медицина | Диагностика и лечение |
Гармонические колебания и токи играют важную роль в современной науке и технологии. Их понимание позволяет улучшить работу электрических систем, разрабатываемых для различных областей применения, и создавать новые инновационные решения.
Напряжение и его влияние на уравнения гармонических колебаний

Напряжение является основной характеристикой электрической цепи и играет важную роль в уравнениях гармонических колебаний. Напряжение может быть постоянным или переменным, и в зависимости от этого меняется форма уравнений колебаний.
В случае переменного напряжения уравнения гармонических колебаний имеют следующий вид:
- Магнитная индукция B пропорциональна силе тока I, возникающей в цепи по закону Ампера.
- Сила тока I пропорциональна напряжению U, возникающему в цепи по закону Ома.
- Напряжение U можно выразить через магнитную индукцию B и площадь петли S, охватывающей проводник, по формуле U = BS.
Таким образом, в уравнениях гармонических колебаний переменный ток и напряжение связаны между собой и зависят от магнитной индукции и площади петли. Из этих уравнений можно получить значения тока и напряжения в зависимости от времени и других физических параметров.
Одной из важных особенностей уравнений гармонических колебаний с переменным напряжением является наличие частоты колебаний. Частота колебаний определяет скорость изменения напряжения и тока в цепи. Частота измеряется в герцах (Гц) и равна количеству полных колебаний в секунду.
Влияние напряжения на уравнения гармонических колебаний проявляется в изменении амплитуды и фазы колебаний. Амплитуда колебаний определяет максимальное значение напряжения и тока в цепи, а фаза колебаний указывает на сдвиг во времени между пиками напряжения и тока.
Таким образом, напряжение играет важную роль в уравнениях гармонических колебаний, определяя форму и характеристики колебаний. Изучение этих уравнений позволяет более глубоко понять физические процессы, происходящие в электрических цепях.
Вопрос-ответ

Что такое гармонические колебания?
Гармонические колебания - это особый вид колебаний, характеризующийся периодическим изменением величины вокруг равновесной точки с постоянной частотой и амплитудой.
Какое уравнение описывает гармонические колебания?
Уравнение гармонических колебаний имеет вид: x(t) = A * cos(ωt + φ), где x(t) - смещение относительно равновесной точки, A - амплитуда колебаний, ω - угловая частота колебаний, t - время, φ - начальная фаза колебаний.
Какое применение имеют гармонические колебания?
Гармонические колебания широко применяются в физике, электронике и технике. Они используются для описания колебательных систем, таких как маятники, электрические колебательные контуры, звуковые волны и др. Гармонические колебания также находят применение в синусоидальных сигналах, используемых в электротехнике и электронике.
Какие силы могут вызывать гармонические колебания тока или напряжения?
Силы, вызывающие гармонические колебания тока или напряжения, могут быть разнообразными. Например, это могут быть силы, возникающие при взаимодействии электрического поля и зарядов, или силы, связанные с магнитным полем и движением зарядов. Важно отметить, что в качестве силы может выступать источник переменного напряжения или тока, создающий осцилляции в электрической цепи.