При работе с электрическими схемами часто возникает необходимость соединить несколько сопротивлений и найти напряжения на каждом из них. Процедура решения таких задач может быть достаточно сложной, особенно когда количество и/или взаимосвязь сопротивлений затрудняют рассмотрение схемы в целом. Однако, для таких случаев существует определенный метод, основанный на использовании схемы звезды.
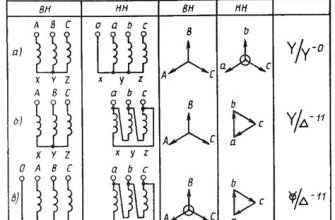
Схема звезды представляет собой соединение трех или более сопротивлений в замкнутую цепь в форме звезды. При этом одна из вершин звезды остается незамкнутой, и к ней подключается источник напряжения. Остальные вершины звезды соединены с источником и друг другом. Такая схема позволяет упростить задачу нахождения напряжений на каждом сопротивлении.
В процессе решения задачи с помощью схемы звезды необходимо перейти к так называемой эквивалентной схеме, где все сопротивления заменены их эквивалентными значениями. Это позволяет построить простую систему уравнений и найти значения напряжений. Также, при использовании схемы звезды можно применять закон Ома, чтобы найти силу тока, а затем использовать закон Кирхгофа для нахождения напряжений на каждом отдельном сопротивлении.
Внутренняя схема звезды

Внутренняя схема звезды - это конфигурация соединения электрических сопротивлений, при которой все точки соединения сопротивлений подключены к одной общей точке, называемой "центром звезды".
В схеме звезды каждое сопротивление представлено отдельной ветвью, которая соединяется с центром звезды. Таким образом, получается "звездная" форма соединения, где центр звезды представляет собой общую точку для всех сопротивлений.
Внутренняя схема звезды широко используется в электротехнике и электронике для соединения сопротивлений, например, в электрических сетях, электрических цепях и схемах коммутации.
Для определения напряжений при соединении сопротивлений в схеме звезды, необходимо использовать законы Кирхгофа, а именно первый и второй законы. Первый закон Кирхгофа утверждает, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из этого узла.
Второй закон Кирхгофа утверждает, что сумма падений напряжения в замкнутом контуре равна сумме электро-ДДЭнных напряжений в этом контуре.
Используя эти законы, можно определить значения напряжений в каждой ветви схемы звезды и общее напряжение в центре звезды.
Таким образом, внутренняя схема звезды представляет собой эффективный и удобный способ соединения сопротивлений, позволяя определить напряжения в каждой ветви схемы и контролировать электрический поток в электрических цепях и схемах.
Значение сопротивлений

Сопротивление – это электрическая характеристика материала, которая определяет его способность сопротивляться току. Измеряется в омах (Ω). Влияет на величину тока, протекающего через цепь, и напряжение, падающее на сопротивлении.
Значение сопротивления зависит от физических свойств материала, длины и площади поперечного сечения проводника. Чем длиннее проводник и меньше его площадь поперечного сечения, тем больше сопротивление. Физические свойства материала могут быть постоянными или зависеть от температуры.
Сопротивления обычно обозначают символом R и указывают его величину в омах. Например, R = 100 Ω.
Сопротивления могут соединяться последовательно или параллельно. В последовательном соединении общее сопротивление равно сумме всех сопротивлений. В параллельном соединении общее сопротивление обратно пропорционально сумме обратных величин сопротивлений.
| Тип соединения | Значение сопротивлений |
| Последовательное | Сумма сопротивлений |
| Параллельное | Обратно пропорционально сумме обратных величин сопротивлений |
Знание значений сопротивлений и способов их соединения позволяет правильно расчитывать напряжения и токи в электрических цепях и создавать электронные устройства с заданными характеристиками.
Вычисление общего сопротивления

Общее сопротивление схемы звезды можно вычислить по формуле:
1/Req = 1/R1 + 1/R2 + 1/R3
где:
- Req - общее сопротивление схемы,
- R1, R2, R3 - сопротивления каждого отдельного резистора.
Для точного учета сопротивлений резисторов в схеме звезды, необходимо сначала вычислить обратные значения сопротивлений каждого резистора, а затем сложить их и взять обратное значение.
Пример:
| Резистор | Сопротивление, Ом |
|---|---|
| R1 | 10 |
| R2 | 20 |
| R3 | 30 |
Вычислим общее сопротивление:
- 1/R1 = 1/10 = 0.1
- 1/R2 = 1/20 = 0.05
- 1/R3 = 1/30 = 0.0333
Сложим обратные значения:
- 0.1 + 0.05 + 0.0333 ≈ 0.1833
Возьмем обратное значение:
- 1/0.1833 ≈ 5.4545
Таким образом, общее сопротивление данной схемы звезды составляет около 5.4545 Ом.
Вычисление общего сопротивления позволяет определить эффективное сопротивление схемы звезды и использовать его для дальнейших расчетов и анализа работоспособности схемы.
Формула для соединения сопротивлений

При соединении сопротивлений в схеме звезды можно использовать специальную формулу для расчета их общего состояния. Формула выглядит следующим образом:
1/Re = 1/R1 + 1/R2 + 1/R3
Где:
- Re - эквивалентное сопротивление всей схемы;
- R1, R2, R3 - значения сопротивлений, которые соединяются.
Эта формула позволяет найти значение общего сопротивления схемы звезды, зная значения сопротивлений каждого отдельного элемента.
При использовании этой формулы важно помнить о следующих особенностях:
- Значение эквивалентного сопротивления будет всегда меньше значения наименьшего сопротивления в схеме.
- Если одно из сопротивлений в схеме равно нулю, то значение эквивалентного сопротивления также будет равно нулю.
- Если все сопротивления в схеме равны между собой, то значение эквивалентного сопротивления будет равно одному из отдельных сопротивлений, разделенному на количество сопротивлений в схеме.
С помощью формулы для соединения сопротивлений можно просто и быстро рассчитать значения эквивалентного сопротивления в схеме звезды, что позволит оптимизировать работу системы и улучшить ее эффективность.
Расчет напряжений на сопротивлениях

Для расчета напряжений на сопротивлениях в схеме звезды необходимо учитывать не только величину каждого сопротивления, но и их взаимное расположение. Важно понимать, что в схеме звезды существуют три возможных направления тока: направления тока в сопротивлении, направления тока от сопротивления и направления тока к сопротивлению.
Для начала определяем суммарное сопротивление звезды, так как все сопротивления в схеме звезды соединены последовательно. Для этого складываем значения всех сопротивлений: R_total = R1 + R2 + R3.
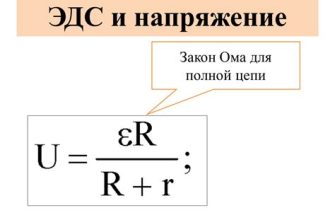
После определения суммарного сопротивления звезды, можно рассчитать напряжение на каждом из сопротивлений. Для этого используем закон Ома, где U = I * R. Учитывая, что сопротивления в схеме звезды соединены параллельно, можно найти общий ток I по закону Кирхгофа: I = U_source / R_total, где U_source - напряжение источника.
Для нахождения напряжения на каждом сопротивлении, умножаем ток I на соответствующие значения сопротивлений: U1 = I * R1, U2 = I * R2, U3 = I * R3.
Таким образом, если известны значения всех сопротивлений и напряжение источника, можно рассчитать напряжения на каждом сопротивлении в схеме звезды.
Вопрос-ответ

Что такое схема звезды?
Схема звезды - это один из способов соединения сопротивлений. В такой схеме все точки сопротивлений соединены в общую точку, которая выступает в качестве "звезды".
Какие преимущества имеет схема звезды перед другими способами соединения сопротивлений?
Схема звезды имеет несколько преимуществ. Во-первых, она позволяет более равномерно распределить напряжение между сопротивлениями, что может быть важно при использовании различных нагрузок. Во-вторых, она облегчает расчеты и анализ цепей с использованием законов Кирхгофа.
Как найти общее сопротивление схемы звезды?
Чтобы найти общее сопротивление схемы звезды, нужно использовать формулу обратного сопротивления, которая выглядит следующим образом: 1/Общее сопротивление = (1/Сопротивление1) + (1/Сопротивление2) + ... + (1/СопротивлениеN). Здесь Сопротивление1, Сопротивление2, ..., СопротивлениеN - сопротивления каждого отдельного элемента.
Как можно использовать схему звезды в практических задачах?
Схема звезды может быть использована в различных сферах. Например, её можно применить для расчета сопротивления в электрических цепях, для определения напряжений при подключении различных нагрузок или при анализе работы источников питания. Кроме того, схема звезды может быть использована для расчета трёхфазных систем или для соединения трансформаторов.