Конденсаторы являются важными элементами электрических цепей, способными хранить электрический заряд. При таком режиме работы, когда конденсатор соединен последовательно с резистором, возникает особый электрический цепь с определенными свойствами.
Одной из важных характеристик такой схемы является напряжение, которое формируется на конденсаторе. Напряжение на конденсаторе зависит от его емкости и сопротивления, которое представляет собой резистор. В данной конфигурации схемы, напряжение на конденсаторе изменяется со временем, проходя через определенный цикл зарядки и разрядки.
Расчет напряжения конденсатора в последовательном соединении с резистором осуществляется на основе принципа зарядки и разрядки конденсатора. Для расчета используются формулы, учитывающие емкость конденсатора, сопротивление резистора, начальное напряжение и время зарядки или разрядки.
Одна из основных формул для расчета напряжения на конденсаторе в такой цепи - это формула времени конденсатора. Она позволяет определить изменение напряжения с течением времени в процессе зарядки или разрядки конденсатора.
Основы напряжения конденсатора

Конденсатор – это электронный компонент, который способен накапливать и хранить электрический заряд. В конденсаторах энергия хранится в виде электрического поля между двумя металлическими обкладками, разделенными диэлектриком.
Напряжение на конденсаторе определяет разность потенциалов между его обкладками и измеряется в вольтах (В). Когда конденсатор заряжается, на нем возникает напряжение, и данный процесс описывается законом Ома.
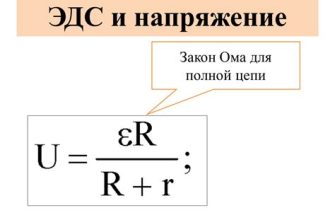
Закон Ома для конденсатора выглядит следующим образом:
- Ток, протекающий через конденсатор, пропорционален скорости изменения напряжения.
- Константа пропорциональности (коэффициент пропорциональности) называется емкостью и обозначается символом C.
- Формула для расчета напряжения на конденсаторе: U = Q/C, где U - напряжение, Q - заряд, C - емкость конденсатора.
Из этой формулы следует, что напряжение на конденсаторе пропорционально заряду и обратно пропорционально емкости. Также следует отметить, что напряжение на конденсаторе не изменяется мгновенно, а меняется с течением времени в соответствии с емкостью и зарядом.
При подключении конденсатора в последовательное соединение с резистором ток начинает протекать через оба элемента. Когда конденсатор заряжается, напряжение на нем увеличивается, а величина тока уменьшается. Этот процесс может быть описан формулой закона Ома для цепи с конденсатором и резистором.
Формула для расчета напряжения в цепи с конденсатором и резистором выглядит следующим образом:
U = U0 (1 - e-t/RC), где U - напряжение на конденсаторе в момент времени t, U0 - исходное напряжение на конденсаторе, t - время, R - сопротивление в цепи, C - емкость конденсатора, e - математическая константа, равная примерно 2.71828.
Из данной формулы следует, что напряжение на конденсаторе в последовательной цепи с резистором изменяется с течением времени и приближается к исходному напряжению со временем, в зависимости от емкости и сопротивления.
Важно отметить, что напряжение на конденсаторе зависит от времени и может быть различным в разные моменты времени. Данные формулы и основные принципы позволяют предсказывать изменения напряжения на конденсаторе в последовательной цепи с резистором и использовать их в различных электронных устройствах.
Подключение конденсатора в цепь

Подключение конденсатора в цепь является одним из основных способов использования этого элемента в электронике. Конденсаторы могут быть подключены в различные типы цепей, включая последовательное и параллельное соединения.
При подключении конденсатора в последовательное соединение с резистором, напряжение на конденсаторе будет зависеть от времени зарядки или разрядки конденсатора через резистор. Заряд конденсатора определяется формулой:
Q = C * V
где Q - заряд конденсатора, C - его емкость, V - напряжение на конденсаторе.
Заряд конденсатора изменяется по формуле:
Q(t) = Q(0) * e^(-t/RC)
где Q(0) - начальный заряд конденсатора, t - время, R - сопротивление резистора, C - емкость конденсатора, e - основание натурального логарифма.
Напряжение на конденсаторе можно определить по формуле:
V(t) = V(0) * e^(-t/RC)
где V(0) - начальное напряжение на конденсаторе, t - время, R - сопротивление резистора, C - емкость конденсатора, e - основание натурального логарифма.
Таким образом, в последовательном соединении конденсатора и резистора, напряжение на конденсаторе будет экспоненциально убывать или возрастать в зависимости от времени.
Принципы последовательного соединения

При последовательном соединении конденсатора и резистора электрическое напряжение (напряжение на конденсаторе) делится между ними пропорционально их сопротивлениям. Это означает, что напряжение на конденсаторе зависит от значения резистора, а также от его собственной емкости.
Если резистор и конденсатор последовательно соединены в цепи, то они образуют RC-цепь. В такой цепи конденсатор оказывает сопротивление переменному току из-за зарядки и разрядки. Зарядка происходит через резистор, поэтому время зарядки конденсатора определяется их взаимным взаимодействием.
Формула для расчета напряжения на конденсаторе в RC-цепи:
| Uc | = U0(1 - e-t/(RC)) |
где Uc - напряжение на конденсаторе в данный момент времени,
U0 - начальное напряжение на конденсаторе (например, в момент time = 0),
t - текущее время,
R - сопротивление резистора,
C - емкость конденсатора.
Из этой формулы видно, что напряжение на конденсаторе растет экспоненциально от заданного начального значения до максимального значения в зависимости от времени и параметров RC-цепи.
При использовании RC-цепи в электронных схемах, таких как фильтры низких частот или задержки времени, важно учитывать время зарядки и разрядки конденсатора. Последовательное соединение конденсатора и резистора позволяет контролировать эти временные характеристики, что делает их полезными компонентами для реализации различных электронных функций.
Влияние резистора на напряжение

В последовательном соединении конденсатора и резистора сначала происходит зарядка конденсатора, а затем установление постоянного напряжения на нем. Резистор в этой схеме играет важную роль и влияет на процесс зарядки и установления напряжения на конденсаторе.
При зарядке конденсатора через резистор ток уменьшается со временем, поскольку заряд конденсатора увеличивается. Это происходит по формуле:
I = V / R,
- I - ток, протекающий через резистор, Ампер (A);
- V - напряжение на конденсаторе, Вольт (V);
- R - сопротивление резистора, Ом (Ω).
Таким образом, напряжение на конденсаторе увеличивается пропорционально продолжительности зарядки и сопротивлению резистора.
В период установления постоянного напряжения на конденсаторе через резистор ток становится равным нулю, и на конденсаторе устанавливается конечное напряжение. Это напряжение можно рассчитать по формуле:
V = V₀(1 - exp(-t / RC)),
- V - напряжение на конденсаторе в момент времени t, Вольт (V);
- V₀ - начальное напряжение на конденсаторе, Вольт (V);
- R - сопротивление резистора, Ом (Ω);
- C - емкость конденсатора, Фарад (F);
- exp(x) - экспонента, функция возведения числа e в степень x.
Из этой формулы видно, что сопротивление резистора влияет на скорость изменения напряжения на конденсаторе и на его окончательное значение. Чем больше сопротивление, тем дольше займет время установления постоянного напряжения на конденсаторе.
Основные формулы и расчет

Рассмотрим основные формулы, необходимые для расчета напряжения при последовательном соединении конденсатора и резистора.
1. Формула для расчета временной постоянной цепи RC:
τ = R * C
где τ - временная постоянная цепи (в секундах), R - сопротивление резистора (в омах), C - емкость конденсатора (в фарадах).
2. Формула для расчета напряжения на конденсаторе в момент времени t:
U(t) = U(0) * (1 - e^(-t/τ))
где U(t) - напряжение на конденсаторе в момент времени t (в вольтах), U(0) - начальное напряжение на конденсаторе (в вольтах), e - число Эйлера (примерное значение 2.71828), t - время (в секундах), τ - временная постоянная цепи.
3. Формула для расчета напряжения на конденсаторе в установившемся режиме:
U(∞) = U(0) * (1 - e^(-t/τ))
где U(∞) - напряжение на конденсаторе в установившемся режиме (в вольтах), U(0) - начальное напряжение на конденсаторе (в вольтах), e - число Эйлера (примерное значение 2.71828), t - время (в секундах), τ - временная постоянная цепи.
4. Формула для расчета времени зарядки конденсатора до определенного напряжения:
t = -τ * ln(1 - (U(t) / U(0)))
где t - время зарядки конденсатора до определенного напряжения (в секундах), τ - временная постоянная цепи, U(t) - напряжение на конденсаторе в момент времени t (в вольтах), U(0) - начальное напряжение на конденсаторе (в вольтах), ln - натуральный логарифм.
Все эти формулы позволяют производить расчеты и определить напряжение на конденсаторе при последовательном соединении с резистором. Они основаны на основных принципах электростатики и электрических цепей.
Примеры практического применения

Последовательное соединение конденсатора с резистором является одной из основных схем в электронике. Ниже приведены примеры практического применения данной схемы.
Блок питания для электронных устройств: в таких блоках питания, например, для зарядки мобильных устройств или питания светодиодных ламп, используется последовательное соединение резистора и конденсатора для стабилизации выходного напряжения. Резистор ограничивает ток, а конденсатор сглаживает пульсации напряжения, обеспечивая стабильное питание устройств.
Фильтр для шумов в сети питания: в электронных устройствах, которые работают от сети переменного тока, используется фильтр для снижения уровня помех и шумов в питающей сети. Фильтр состоит из резистора и конденсатора, соединенных последовательно. Резистор ограничивает ток, а конденсатор сглаживает пульсации напряжения и фильтрует высокочастотные помехи.
Управление яркостью светодиодной подсветки: для регулировки яркости светодиодных ламп и подсветки используется техника ШИМ (широтно-импульсная модуляция). В данной схеме резистор и конденсатор соединяются последовательно с микроконтроллером или драйвером светодиодов. Использование конденсатора позволяет сгладить импульсы напряжения и реализовать плавное изменение яркости светодиодов.
Датчики и измерительные устройства: множество датчиков и измерительных устройств используют последовательное соединение конденсатора и резистора для сглаживания и фильтрации сигналов. Например, при использовании датчиков температуры, давления или влажности, конденсатор и резистор помогают сгладить сигналы и получить более точные измерения.
Вышеперечисленные примеры демонстрируют широкое практическое применение последовательного соединения конденсатора с резистором в различных областях электроники.
Вопрос-ответ

Как рассчитать напряжение на конденсаторе в последовательном соединении с резистором?
Для расчета напряжения на конденсаторе в последовательном соединении с резистором необходимо знать значение емкости конденсатора (C), сопротивление резистора (R) и время (t). Формула расчета напряжения на конденсаторе в таком случае имеет вид V = V0 * (1 - exp(-t/RC)), где V0 - начальное напряжение на конденсаторе.
Как влияет изменение сопротивления резистора на напряжение на конденсаторе в последовательном соединении?
Изменение сопротивления резистора (R) в последовательном соединении с конденсатором приводит к изменению временной константы (τ) этой цепи. Чем больше сопротивление резистора, тем медленнее конденсатор будет заряжаться и разряжаться. Следовательно, напряжение на конденсаторе будет изменяться медленнее при большом сопротивлении и быстрее при малом.
Как влияет изменение емкости конденсатора на напряжение на конденсаторе в последовательном соединении?
Изменение емкости конденсатора (C) в последовательном соединении с резистором приводит к изменению временной константы (τ) этой цепи. Чем больше емкость конденсатора, тем дольше он будет заряжаться и разряжаться при заданном сопротивлении. Таким образом, напряжение на конденсаторе будет изменяться медленнее при большой емкости и быстрее при малой.